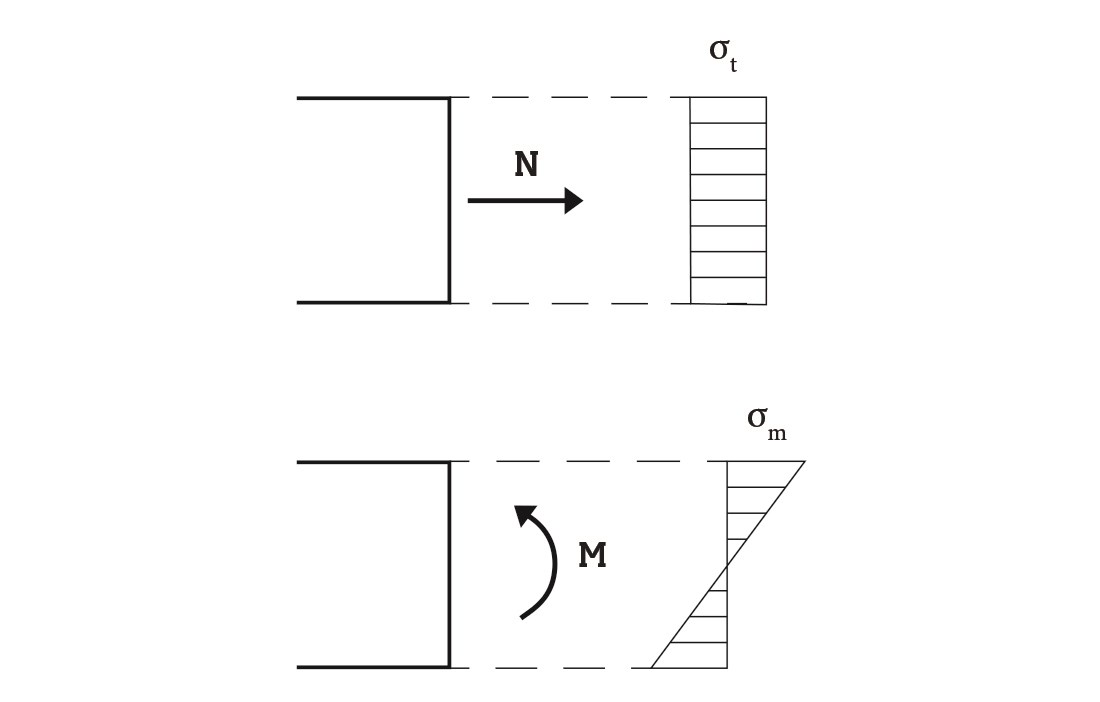
A strong, light sheet – It is hardly surprising that a structural component under an axial load is more effective than the equivalent component under bending stress. This can easily be appreciated by studying the distribution of stresses in a cross-section that is subject to axial force and moment, respectively. As can be seen in figure 1, the stress under an axial load is evenly distributed, which enables full utilisation of the cross-section’s capacity. In the cross-section under bending stress, however, the stress shows a linear distribution. This means that the material’s full capacity can only be achieved in the outer fibres of the cross-section, while the central part of the cross-section remains underutilised.
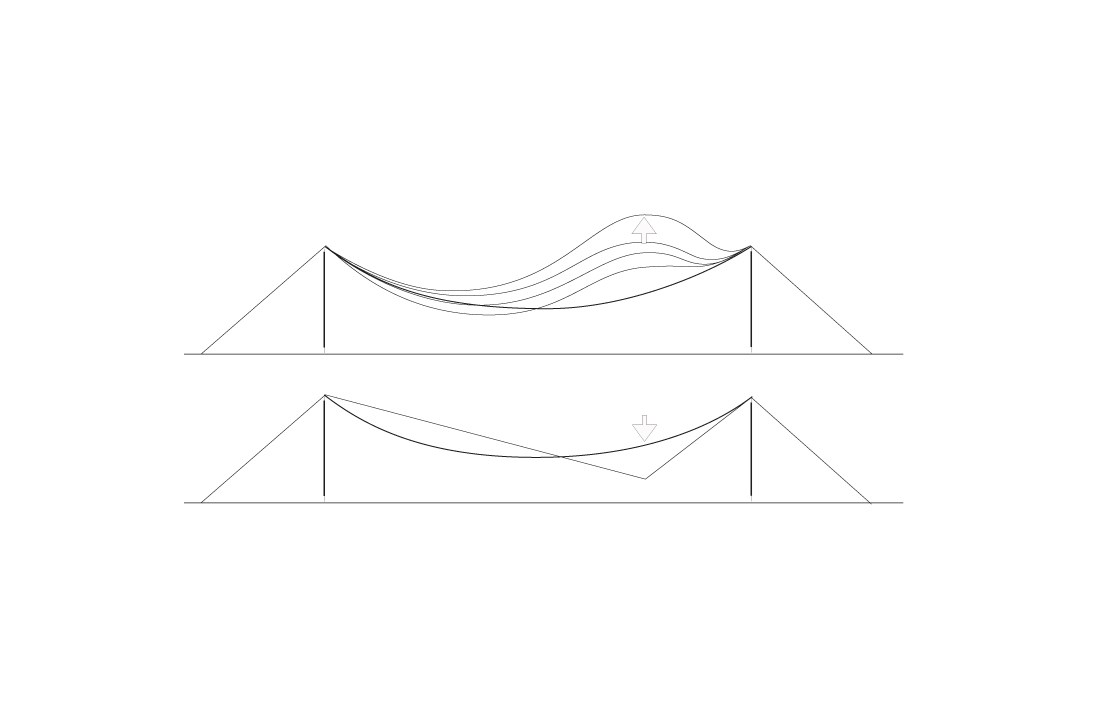
In regular suspension structures, the primary load-bearing duties are discharged by wires or cables. These lack any capacity to take up moment and therefore transfer loads only through tensile stresses in the primary load-bearing structure. In addition, wires and cables lack bending stiffness, which means that the only way these structures can bear a load is by changing their original form. In many cases, this form change can be problematic, particularly for roof structures that are subject to non-symmetrical loads, such as uneven snow load. In such a situation, a flexible suspension structure would be highly likely to suffer unacceptably large deformations. Sensitivity to wind-induced instability – i.e. wind oscillations created by gusts of wind or periodic vortex shedding – is also a common problem in flexible suspension structures, see figure 2.
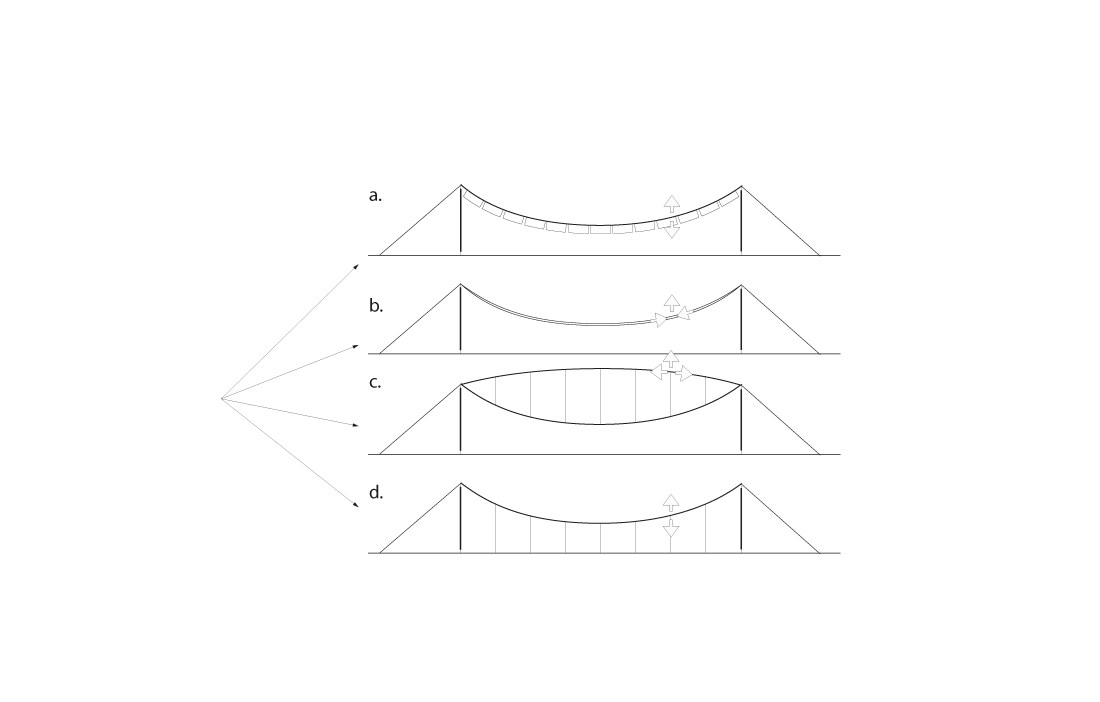
There are, however, a number of methods for stiffening up suspension roof structures and so reducing the risk of large deformations and wind-induced instability. These are illustrated in figure 3.
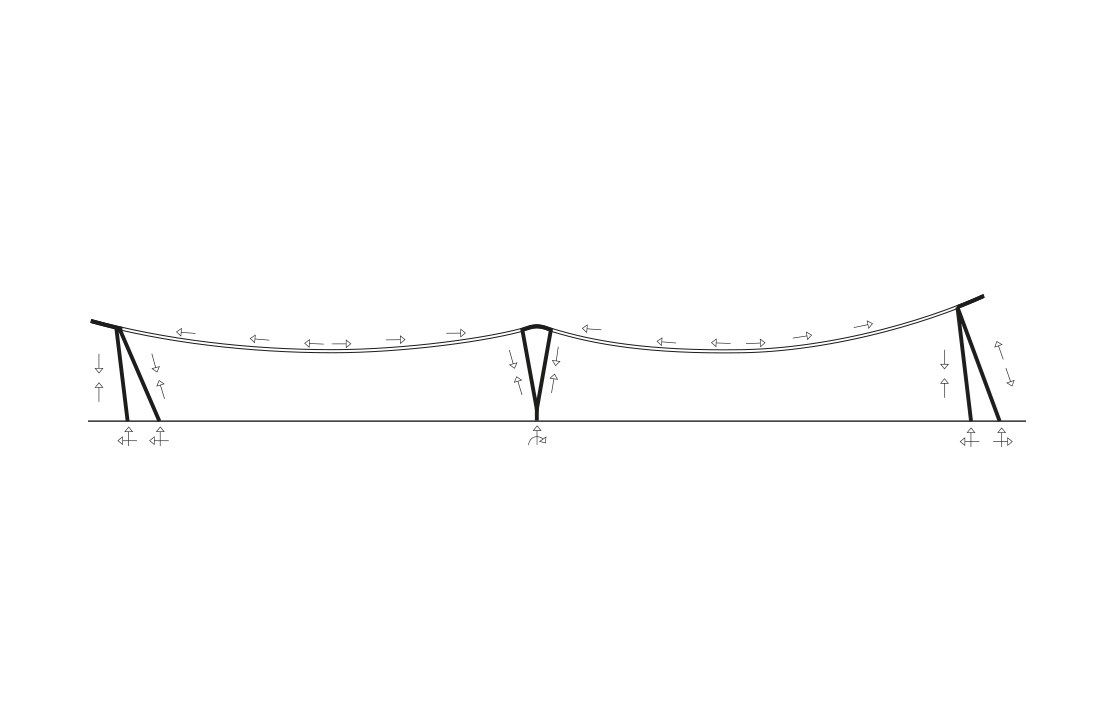
Suspension roof structures where wood is used as the load-bearing structural material are generally designed in line with principle b) in figure 3. This kind of load-bearing system is sometimes called a “stress ribbon”, which in principle is a cable structure with non-negligible bending stiffness. These roof structures traditionally take the form of a second-degree parabola or sometimes a catenary (these geometric curves differ very little, particularly when the degree of sag is small). The ratio between sag and span in a stress ribbon structure is usually put at around 0.10–0.12, which is slightly higher than for regular suspension bridges. Under downward-acting loads, be they permanent loads or snow, the stress ribbon functions more or less like an ordinary cable structure, where the majority of the load is taken up through tension and a much smaller proportion of the load is taken up by bending. The inherent bending stiffness of stress ribbon structures has a beneficial effect in reducing both deformations under non-symmetrical loads and – to a certain extent – the risk of wind-induced instability. In the case of upward loads, such as wind suction, the roof acts as an upturned arch. In this case the load is taken up mainly through compression in the roof structure and so it is important to account for the risk of buckling.
Wood is ideal for stress ribbon structures, since the material has outstanding strength properties, particularly in terms of specific strength, i.e. its strength-to-weight ratio. The disadvantage – on the other hand – is that suspension structures are often subject to major tensile stresses, which means that the choice of suitable wood joints can be a challenge.
Text Roberto Crocetti